Russell Saerang

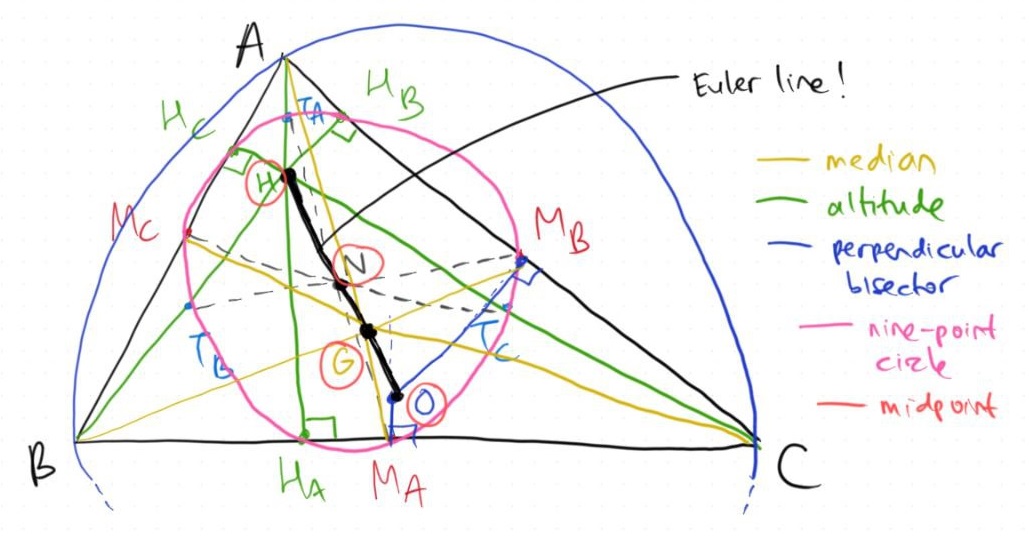
The Nine-point Circle

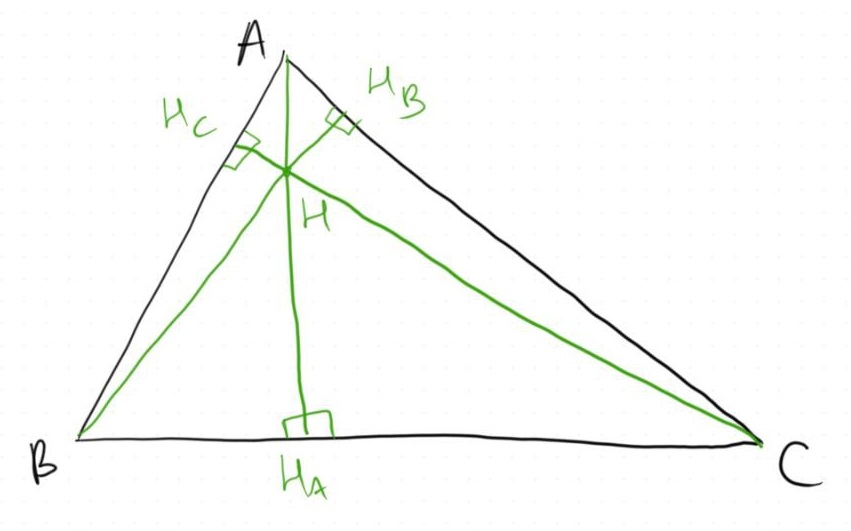
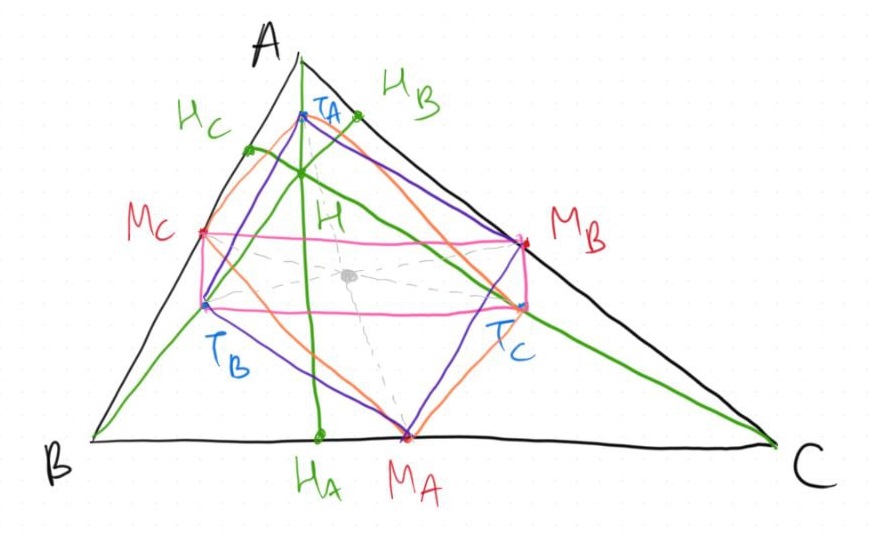
Let us start off with a simple triangle $\triangle ABC$. We draw the altitudes for each respective vertex, intersecting the corresponding sides at $H_A, H_B, H_C$. It is a well-known fact that these three altitudes will intersect at a single point, the orthocenter, denoted as $H$.

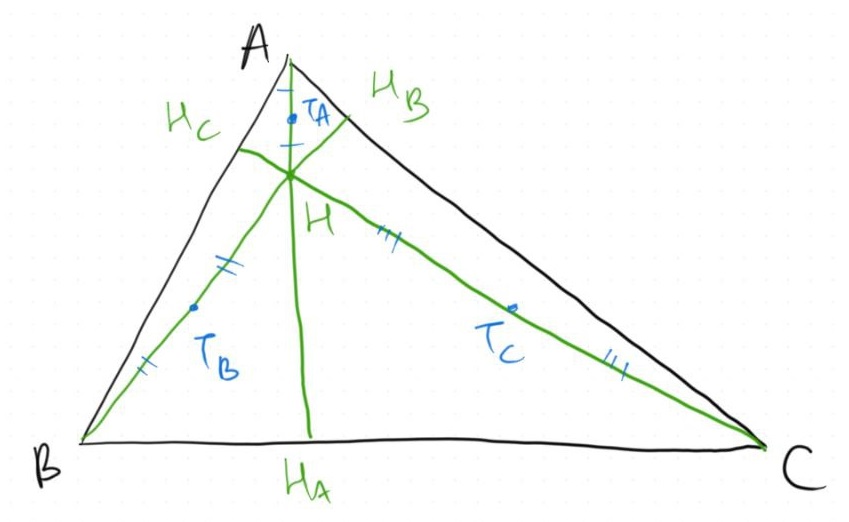
Next, we take the midpoints of $AH_A, BH_B, CH_C$ and denote them as $T_A, T_B, T_C$, respectively.

Finally, the midpoints of $BC, CA, AB$ denoted as $M_A, M_B, M_C$.

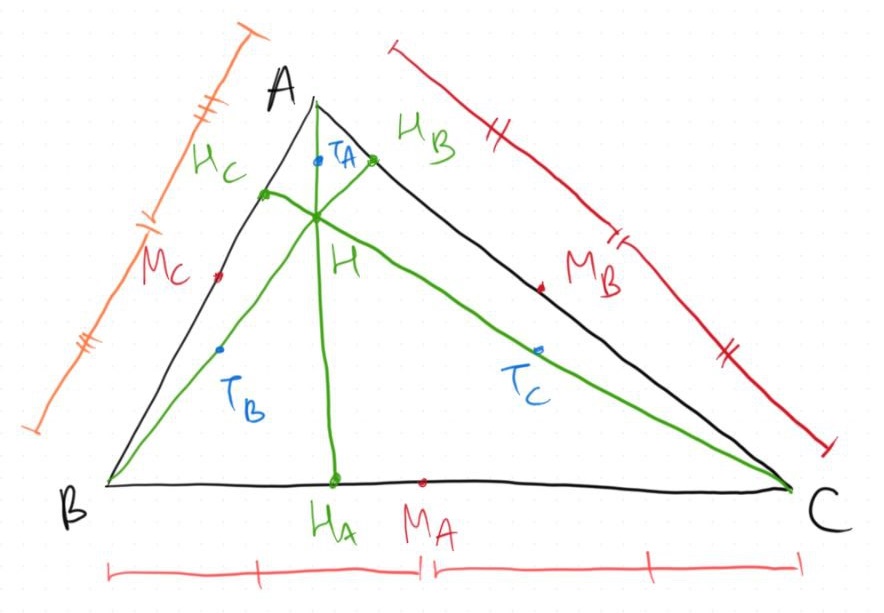
In case you haven't known, the points $H_A,H_B,H_C,M_A,M_B,M_C,T_A,T_B,T_C$ all lie inside a common circle, thus the name nine-point circle. Therefore, let's explore the proof that these nine points indeed lie on a single circle!

The Proof

Let's focus ourselves on $\triangle ABH$. Note that both $M_C$ and $T_B$ are midpoints of $BA$ and $BH$ respectively. Therefore, $M_CT_B \parallel AH$.

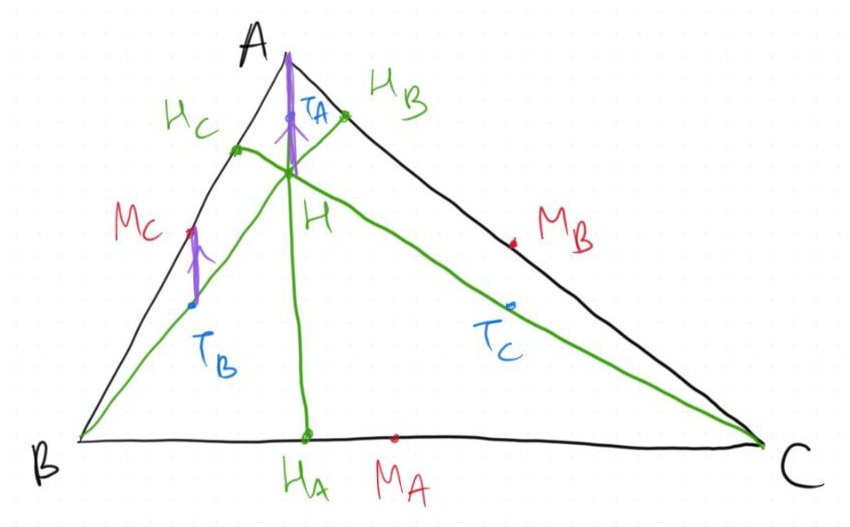
We can use the same idea to prove that $M_BT_C \parallel AH$.

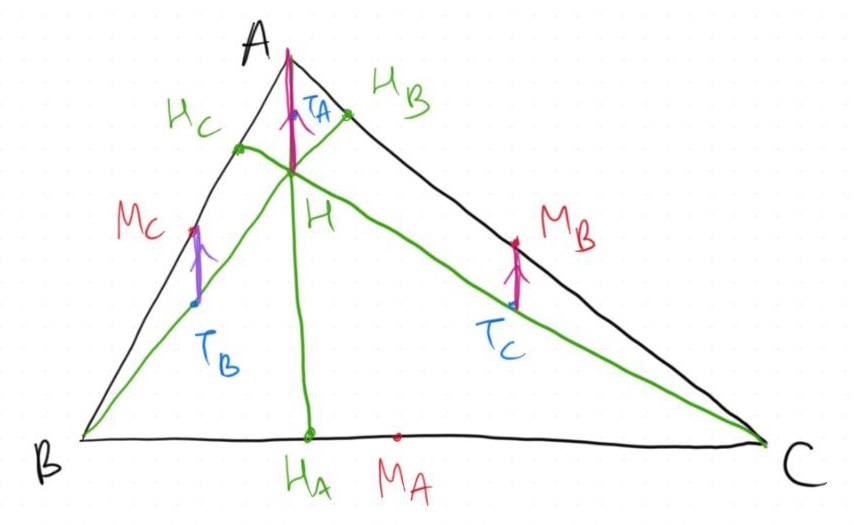
The same idea again to prove that $M_BM_C \parallel BC$ and $T_BT_C \parallel BC$, which also implies $M_BM_C \parallel T_BT_C \perp AH$ due to the fact that $AH$ is the altitude corresponding to $BC$. Thus, both $M_BM_C$ and $T_BT_C$ are perpendicular to both $M_CT_B$ and $M_BT_C$.

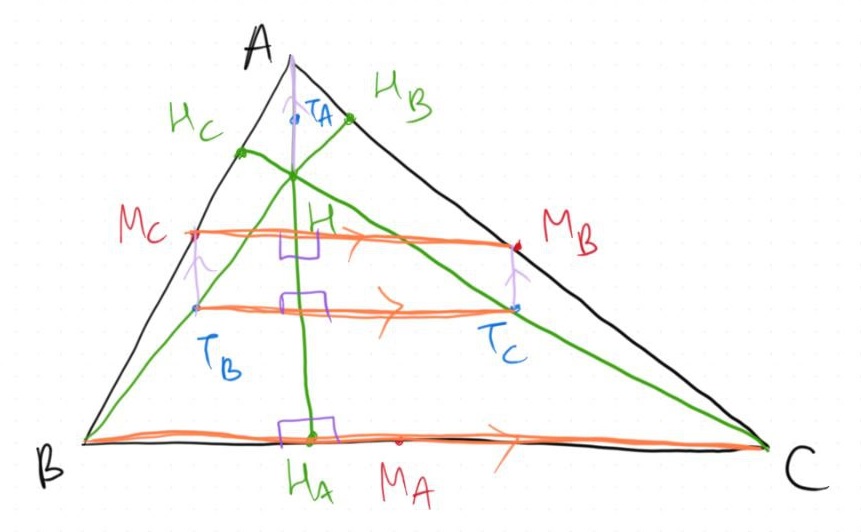
Combining these arguments, we can conclude that $M_BM_CT_BT_C$ is a rectangle!

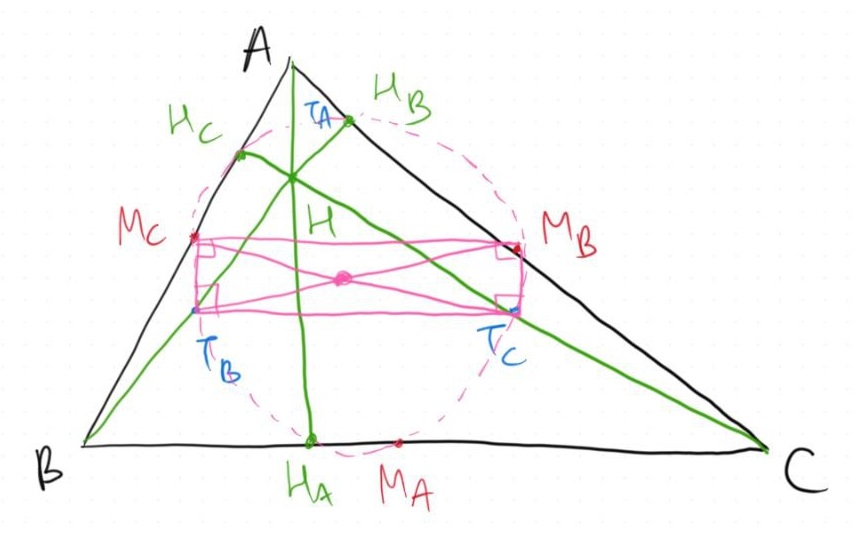
Consider the circle that inscribes $M_BM_CT_BT_C$. SInce $M_BM_CT_BT_C$ is a rectangle, both $M_BT_B$ and $M_CT_C$ are diameters of this circle.

Now, we can repeat these arguments again to prove that $M_AM_BT_AT_B$ and $M_AM_CT_AT_C$ are also rectangles and are inscribed within this same circle because they have common diameters.

Therefore, at this point, we managed to prove that $M_A, M_B, M_C, T_A, T_B, T_C$ all lie on the same circle and we're left with proving that $H_A, H_B, H_C$ also lie on this circle.

This can be done rather quickly because we know that $M_AT_A$ is a diameter of the circle so for any point $X \neq M_A, T_A$ in the circle, $\angle M_AXT_A$ is a right angle. But this is the case for $X = H_A$ because $AH_A \perp BC \parallel H_AM_A$. Therefore, $H_A$ lies on this circle.

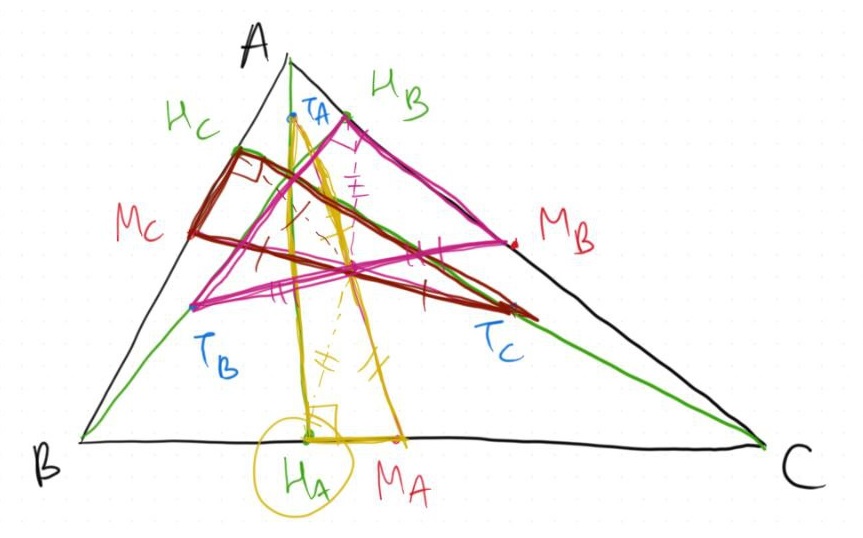
Analogously we can prove that $H_B$ and $H_C$ lie on the circle and therefore our proof is complete!

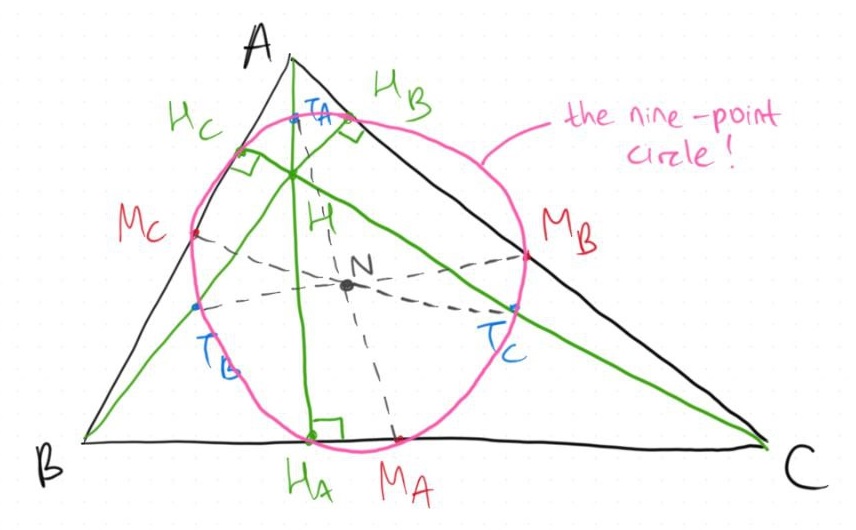
What's Next

There some interesting properties derived from the existence of the nine-point circle. You can easily find these online, but my personal favourite would be the Euler line!

The Euler line of $\triangle ABC$ is a line, that passes through the orthocenter $H$, the centroid $G$, the circumcenter $O$, and the nine-point center $N$ with the following property:

$$OG:GN:NH = 2:1:3$$

While the proof might be out of scope, I would like to keep this article short and simple as the main purpose is to appreciate how we can construct such well-worded arguments to proof the existence of the nine-point circle!